উপরের চিত্রে, AB ও CD দুটি সমান্তরাল সরলরেখা এবং EF' সরলরেখাগুলোকে যথাক্রমে দুটি বিন্দু Pওতে ছেদ করেছে। EF সরলরেখা AB ও CD সরলরেখাদ্বয়ের ছেদক। ছেদকটি AB ও CD সরলরেখা দুটির সাথে ∠1,∠2,∠3,∠4,∠5,∠6.∠7.∠8 মোট আটটি কোণ তৈরি করেছে। এ কোণগুলোর মধ্যে
(ক) ∠ 1 এবং ∠ 5 , ∠ 2 এবং ∠ 6 , ∠ 3 এবং ∠ 7 , ∠ 4 এবং ∠ 8 পরস্পর অনুরূপ কোণ।
(খ) ∠ 3 এবং ∠ 6 ∠ 4 এবং ∠ 5 হলো পরস্পর একান্তর কোণ।
(গ) ∠ 3 ∠ 4 ∠ 5 ∠ 6 অন্তঃস্থ কোণ।
এই একান্তর ও অনুরূপ কোণগুলোর মধ্যে সম্পর্ক রয়েছে। এই সম্পর্ক বের করার জন্য দলগতভাবে নিচের কাজটি কর।
কাজ: ১। রুলটানা একপৃষ্ঠা কাগজে চিত্রের ন্যায় দুটি সমান্তরাল সরলরেখা ও এদের একটি ছেদক আঁক। দুই জোড়া অনুরূপ কোণ চিহ্নিত কর। প্রতিজোড়া অনুরূপ কোণ সমান কিনা যাচাই কর। সমান হয়েছে কি? ২। দুই জোড়া একান্তর কোণ চিহ্নিত কর। প্রতি জোড়া একান্তর কোণ সমান কিনা যাচাই কর। সমান হয়েছে কি? ৩। সমান্তরাল সরলরেখাদ্বয়ের ছেদকের একই পাশের অন্তঃস্থ কোণ দুটি পরিমাপ কর। কোণ দুটির পরিমাপের যোগফল বের কর। যোগফল তোমার সহপাঠীদের বের করা যোগফলের সাথে তুলনা কর। তোমাদের যোগফল সামান্য কম-বেশি 180° কিন্তু হয়েছে কি?  |
কাজের ফলাফল পর্যালোচনা করে আমরা নিচের সিদ্ধান্তে উপনীত হই:
|
সমান্তরাল সরলরেখার এই তিনটি ধর্ম (property) আলাদাভাবে প্রমাণ করা যায় না। এরা প্রত্যেকেই ইউক্লিডের ৫ম স্বীকার্যের বিভিন্ন রূপ। এদের যেকোনো একটিকে সমান্তরাল সরলরেখার সংজ্ঞা হিসেবে বিবেচনা করলে বাকি দুটি ধর্ম ব্যাখ্যা করা যায়। অর্থাৎ, যদি এই তিনটি ধর্মের যেকোনো একটিকে সত্য ধরে অপর দুটি ধর্মকে ব্যাখ্যা করা যায়, তবে প্রথমে বিবেচিত সংজ্ঞাটিকে আমরা সঠিক বলে ধরে নিতে পারি
সমান্তরাল সরলরেখার একটি ধর্ম: দুটি সমান্তরাল সরলরেখার একটি ছেদক দ্বারা উৎপন্ন প্রত্যেক অনুরূপ কোণ জোড়া সমান-কে সত্য ধরে নিয়ে সমান্তরাল সরলরেখার আরেকটি ধর্মকে নিচে ব্যাখ্যা করা হলো।
দুটি সমান্তরাল সরলরেখার একটি ছেদক দ্বারা উৎপন্ন একান্তর কোণের সম্পর্ক:
দুটি সমান্তরাল সরলরেখাকে একটি সরলরেখা ছেদ করলে একান্তর কোণ জোড়া সমান।
বিশেষ নির্বচন: মনে করি, AB || CD এবং PQ ছেদক তাদের যথাক্রমে E ও F বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, ∠LAEF = একান্তর ∠EFD
প্রমাণ:
ধাপ:
(১) ∠PEB = অনুরূপ ∠EFD
(২) ∠PEB = বিপ্রতীপ ∠AEF
∴ ∠AEF = ∠EFD
[প্রমাণিত]
যথার্থতা
[সমান্তরাল রেখার সংজ্ঞানুসারে অনুরূপ কোণ সমান]
[বিপ্রতীপ কোণদ্বয় পরস্পর সমান। [(১) ও (২) থেকে
| কাজ ১। প্রমাণ কর যে, দুটি সমান্তরাল সরলরেখার একটি ছেদক দ্বারা উৎপন্ন ছেদকের একই পাশের অন্তস্থ কোণদ্বয়ের সমষ্টি দুই সমকোণের সমান। |
চিত্রে, AB || CD এবং PQ ছেদক তাদের যথাক্রমে Eও F বিন্দুতে ছেদ করেছে।
সুতরাং, (ক)∠PEB = অনুরূপ ∠EFD
(খ) ∠AEF = একান্তর ∠EFD
(গ) ∠BEF + ∠EFD = দুই সমকোণ।
কাজ ১। একটি সরলরেখার উপর দুটি বিন্দু নাও। রেখাটির বিন্দু দুটিতে একই দিকে 60° এর সমান দুটি কোণ আঁক। কোণদ্বয়ের অঙ্কিত বাহু দুটি সমান্তরাল কিনা যাচাই কর। ২। 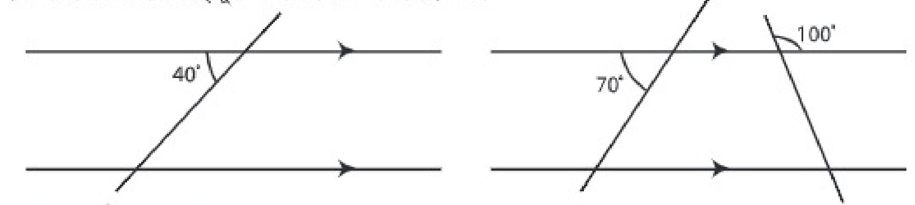 চিত্রে ছেদক দ্বারা উৎপন্ন কোণগুলোর মান বের কর। |
|
চিত্রে, AB ও CD রেখাদ্বয়কে PQ রেখা যথাক্রমে Eও F বিন্দুতে ছেদ করেছে এবং
(ক) ∠AEF = একান্তর ∠EFD
অথবা, (খ) ∠PEB = অনুরূপ ∠EFD
অথবা, (গ) ∠BEF + ∠EFD = দুই সমকোণ।
সুতরাং, AB ও CD রেখা দুটি পরস্পর সমান্তরাল।
common.read_more
common.or
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
